Search settings specific to models in specialized shape contexts
- See also

 Availability
Availability

 Previous
Previous
- Next

MIL supports context types for specialized shape searches. Besides supporting many search settings supported for equivalent predefined-shape models in M_GEOMETRIC and M_GEOMETRIC_CONTROLLED types of Model Finder contexts, a predefined shape model in an M_SHAPE_... context supports additional search settings, specific to their model type.
Radii deviation tolerance
For a model in an M_SHAPE_CIRCLE or M_SHAPE_ELLIPSE type of Model Finder context, you can adjust the sagitta tolerance (MmodControl() with M_SAGITTA_TOLERANCE) to limit the allowable radii deviation from the defined conic shape (circle of ellipse). Given the other specified constraints for the model, there is a certain amount of deviation that can be permitted. Using M_SAGITTA_TOLERANCE, you can restrict this amount. Essentially, M_SAGITTA_TOLERANCE establishes the search area in which to consider active edges for an occurrence at a given scale; a best fit conic is then fit within these active edges.
For a model in an M_SHAPE_CIRCLE type of Model Finder context, the sagitta tolerance allows you to specify how perfectly circular you want the occurrence to be. This allows you to find circular shapes that do not have a constant radius over the full angular range of the contour. For instance, an elliptical shape could be identified as a potential occurrence if the radii variation is within the bounds specified using M_SAGITTA_TOLERANCE.
More generally, the sagitta tolerance allows to identify shapes that are elliptical (or circular) in nature, but have rough or noisy edges, such as a bottle cap, could be identified as a potential occurrence of a circle. If the occurrence in the target is expected to be perfectly circular with a constant radius across the full angular range, you could safely set the sagitta tolerance close to 0.0%. Whereas, if the typical occurrence within a target does not contain a perfectly smooth contour, such as containing rough edges, this control type should be increased from the default value of 25.0%.
The following two images deal with trying to identify an elliptical shape as an occurrence of a circle model. In the image on the left, you can see that the algorithm found the edge of the ellipse but, because the selected sagitta tolerance was set too low, the center of the search area does not coincide with the center of the occurrence being sought. In the image on the right, you can see that the ellipse falls completely within the upper and lower bounds of the search area established by the sagitta tolerance, and as such the occurrence being sought is found.


The model coverage for the image on the left would be relatively low, never reaching 50%. Whereas the model coverage for the image on the right would be near 100%. This is because the contour being sought is completely within the bounds of the search area defined by the sagitta tolerance for the image on the right; so, the entire contour is considered an active edge of the occurrence. For the image on the left, the bounds of the search area defined by the sagitta tolerance do not encompass the ellipse entirely, so only the portion of the contour within the bounds is considered as an active edge of the occurrence. In contrast, the fit error for the image on the left would be small, while the image on the right would have a much higher fit error. This is because the returned occurrence (best fit circle) for the image on the left coincides closely with the portion of the ellipse within the search area, whereas the returned occurrence for the image on the right only has 4 intersection points with the ellipse.
The following images demonstrate a situation where the outline of a flower needs to be identified as an occurrence. In the image on the left, the sagitta tolerance was set too low, causing the algorithm to identify the outline of the petal as being the circular shape being sought. In the image on the right, the sagitta tolerance was set to an appropriate level, and the average outline of the flower was identified as an occurrence.


The model coverage for the image on the left would be roughly 50% while the coverage for the image on the right would be near 100%. Much like for the elliptical example, the contour being sought is completely within the bounds of the sagitta tolerance for the image on the right; while for the image on the left, the bounds of the sagitta tolerance encompass only one petal of the flower. The fit error for the image on the left would be much lower than that for the image on the right. This is because the returned occurrence for the image on the left corresponds strongly with the portion of the flower within the search area; while for the image on the right, the returned occurrence does correspond closely with the contour being sought, but due to the nature of the contour (not perfectly circular), there will always be a fit error.
The following images demonstrate cases where the sagitta tolerance was set to an appropriate level and where it was set to be too high. The image on the left demonstrates a case where the sagitta tolerance was set to an appropriate level and the occurrence of the circular shape was accurately detected. The image on the right demonstrates a case where the sagitta tolerance was set to an exceedingly high level. It can be seen that the upper bound of the sagitta tolerance covers the edge of an adjacent rectangle, and as such, the edge of the rectangle is misidentified as being a part of the occurrence being sought.


Although the model coverage would be high, over 75%, in the two images above, the model coverage for the image on the right would actually be higher than that on the left. This is because the algorithm detects the edges of the rectangle as being the missing edges. There are still some edges which are missing for the model on the right (from +/- 25 o to +/- 30 o ); this means that the model coverage will never be 100%. The fit error for the image on the left would be very low since the model's active edges coincide highly with the edges of the contour being sought. In contrast, the fit error for the image on the right would be higher since the occurrence does not have as close a fit with the active edges.
Aspect ratio and aspect ratio search constraint
For a model in an M_SHAPE_ELLIPSE type of Model Finder context, you can set the nominal aspect ratio at which you expect to find the occurrence in the target. This is useful, for example, if an elliptical object might appear shorter because of perspective and you can't perform camera calibration. To do so, set the factor to apply to the model's aspect ratio so that it matches the nominal aspect ratio of the occurrence, using MmodControl() with M_MODEL_ASPECT_RATIO; this is referred to as the nominal aspect ratio factor. It is applied as follows.
Effective aspect ratio = Nominal aspect ratio factor x (Model width/Model height).
Note that to change the effective aspect ratio of the model, MIL internally changes the effective height of the model; the effective width of the model is not modified. That is, the nominal aspect ratio factor is inversely applied to the height of the model.
Effective model height = Model height / Nominal aspect ratio factor .
If you want to search for occurrences of the model that have the established effective aspect ratio, but are wider than the original model's width, you must adjust the model's scale using M_SCALE.

For a model in an M_SHAPE_ELLIPSE type of Model finder context, the occurrence's aspect ratio is calculated such that its width is the length of its longest side and its height of the shorter side, regardless of the occurrence's orientation; therefore the occurrence will always have an aspect ratio greater than or equal to 1. As such, the aspect ratio of the model, multiplied by the nominal aspect ratio factor must be greater than or equal to 1. To use the minimum allowable value for the nominal aspect ratio factor, you can set M_MODEL_ASPECT_RATIO to M_CIRCLE_ASPECT_RATIO. This will ensure that the final aspect ratio is equal to 1.
You can also specify a range of aspect ratios that the occurrence can have. To do so, you specify the minimum and maximum factors with which to multiply the nominal aspect ratio factor, using MmodControl() with M_MODEL_ASPECT_RATIO_MAX_FACTOR and M_MODEL_ASPECT_RATIO_MIN_FACTOR. The minimum factor and maximum factor together determine the aspect ratio range from the nominal aspect ratio (M_MODEL_ASPECT_RATIO).
Maximum effective aspect ratio = (M_MODEL_ASPECT_RATIO) x (M_MODEL_ASPECT_RATIO_MAX_FACTOR) x (Model width / Model height).
Minimum effective aspect ratio = (M_MODEL_ASPECT_RATIO) x (M_MODEL_ASPECT_RATIO_MIN_FACTOR) x (Model width / Model height).
These also only affect the effective height of the model.
For example, if you define your model to have both a width and length of 5, the model's aspect ratio is therefore 1. Setting the M_MODEL_ASPECT_RATIO control type to 2, and leaving the M_MODEL_ASPECT_RATIO_MIN_FACTOR and M_MODEL_ASPECT_RATIO_MAX_FACTOR control types to their default values of 0.8 and 1.2 respectively, corresponds to an aspect ratio range from 1.6 to 2.4.

If you defined a model having a height of 5 and a width of 10, its aspect ratio would be 2. If the M_MODEL_ASPECT_RATIO, M_MODEL_ASPECT_RATIO_MIN_FACTOR, and M_MODEL_ASPECT_RATIO_MAX_FACTOR control types are left to their default values of 1, 0.8, and 1.2 respectively, this corresponds to an aspect ratio range from 1.6 to 2.4. However, if the M_MODEL_ASPECT_RATIO control type was set to 2, and the M_MODEL_ASPECT_RATIO_MIN_FACTOR and M_MODEL_ASPECT_RATIO_MAX_FACTOR control types are still left to their default values of 0.8 and 1.2 respectively, this corresponds to an aspect ratio range from 3.2 to 4.8.

Note that the range is defined as factors so that if you change the nominal aspect ratio factor (M_MODEL_ASPECT_RATIO), you do not have to modify the range settings. As the factors increase in value, the height of the effective model is reduced proportionally. Furthermore, the minimum effective aspect ratio should be greater than or equal to 1. If M_MODEL_ASPECT_RATIO_MIN_FACTOR is set such that it would lead the minimum effective aspect ratio to be less than 1, MIL will internally set the control type to M_CIRCLE_ASPECT_RATIO.
Instead of excluding a candidate that falls outside the aspect ratio range, you can constrain its fit. This candidate will have its fit constrained to the closest bound of the aspect ratio range, will have its score reduced accordingly, but will still be identified as a candidate. To do so, use MmodControl() with M_SEARCH_ASPECT_RATIO_CONSTRAINT set to M_ENABLE, which is the control type's default value. When disabled, only candidates that are within the bounds established using the maximum and minimum factors can be returned as occurrences.
For example, if the aspect ratio range was from 1.6 to 2.4 and M_SEARCH_ASPECT_RATIO_CONSTRAINT control type was set to M_DISABLE, a candidate with an aspect ratio of 2.6 would not be identified as a candidate. However, the candidate would be identified as a possible occurrence if the M_SEARCH_ASPECT_RATIO_CONSTRAINT control type was set to M_ENABLE; in this case, the candidate would have a reduced score, and its aspect ratio would be constrained to 2.4 (that is, reported as being 2.4).
Deviation tolerance for rectangles and segments
For a model in an M_SHAPE_RECTANGLE or an M_SHAPE_SEGMENT type of Model Finder context, you can adjust the deviation tolerance (M_DEVIATION_TOLERANCE) to limit the allowable deformation from the defined rectangle or segment. This sets the tolerance of the deformation of rectangles and line segments such that rectangles or segments that are not perfectly straight, or rectangles or segments that are broken up, would still be identified as potential occurrences. Given the other specified constraints for the model, there is a certain amount of deviation that can be permitted. Using M_DEVIATION_TOLERANCE, you can restrict this amount.
Angle for rectangles and segments
As with other model types, you can specify the nominal angle and angular range at which to search for a model in an M_SHAPE_RECTANGLE or M_SHAPE_SEGMENT Model Finder context, using MmodControl() with M_ANGLE and M_ANGLE_DELTA... control types, respectively.
For an M_SHAPE_SEGMENT context, Model Finder searches for segment occurrences along contours, so the segment's angle (direction) is determined from contour's gradient angle (the direction of the most sudden change from dark to light causing the edge). The segment's angle is the angle of the gradient - 90°.

Note that a rectangle at a specified angle, M_ANGLE, and a rectangle at M_ANGLE + 180° are the same rectangle.
Due to the symmetry of rectangle and segment models and the search algorithm used when defined in a shape-specific context, you can search within multiple angular ranges, without defining additional contexts and performing additional searches, using M_ANGLE_MULTIPLE_RANGE. This allows you to search for occurrences at the nominal angle and at the angle perpendicular to this angle simultaneously (M_STEP_90). In the case of a segment model, you can also search for occurrences with opposite segment gradient directions (M_STEP_180).
Calculations specific to angle-range search strategies are not necessary; as such, M_SEARCH_ANGLE_RANGE is not supported.
A segment occurrence can run the length of a contour that transitions between 180° opposing gradient directions (for example, along an edge of a chessboard grid row), as long as part of the segment meets the angle requirements along the contour. The segment occurrence is reported to have the angle closest to the angle being sought. For example, if searching at a nominal angle of 0° and a segment along a contour transitions between 0° and 180°, the segment is returned as an occurrence and is reported to have an angle of 0°. To force Model Finder to find segment occurrences that have an appropriate angle along their entire length, enable M_SEGMENT_CONSISTENT_GRADIENT. The following animation illustrates how M_SEGMENT_CONSISTENT_GRADIENT influences what is returned as an occurrence.
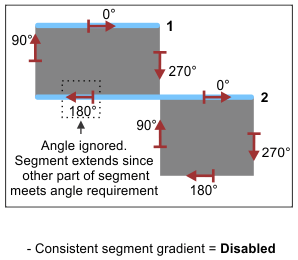

When searching for segments in an image with lines, each line is counted as two occurrences with opposite angles. You can restrict what is returned to one occurrence by setting MmodControl() with M_MIN_SEPARATION_ANGLE to M_DISABLE.
