Custom spatial filters
- See also

 Availability
Availability 
 Previous
Previous
- Next

-
If the width (SizeX) of the kernel is an odd number, the X-coordinate is (SizeX-1)/2.
-
If the width (SizeX) of the kernel is an even number, the X-coordinate is (SizeX/2)-1.
-
Allocate a kernel buffer, using MbufAlloc1d() or MbufAlloc2d() with M_KERNEL. The kernel size is specified when allocating the kernel buffer. Note that the kernel size can be constrained by the available resources.
-
Load the required kernel values into this kernel buffer, using MbufPut() or MbufPut2d().
-
If required, modify the setting of the operation control types associated with your custom filter, using MbufControl(). The operation control types determine how the convolution operation will be performed. You can control:
-
Whether or not the absolute value of the result is taken (M_ABSOLUTE_VALUE).
-
The division (normalization) factor to apply to the result (M_NORMALIZATION_FACTOR).
-
Whether or not to saturate the result (M_SATURATION).
-
The position of the center pixel (M_OFFSET_CENTER_X and M_OFFSET_CENTER_Y).
-
How the operation handles the borders (overscan) of the source buffer (M_OVERSCAN and M_OVERSCAN_REPLACE_VALUE). If overscan is disabled, the border pixels of the source image are not processed if additional processing time is needed.
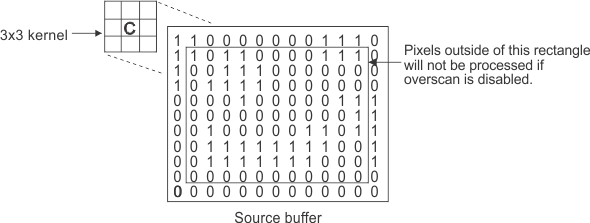
-
-
Allocate a linear IIR filter context, using MimAlloc() with M_LINEAR_FILTER_IIR_CONTEXT.
-
Use MimControl() and specify appropriate M_FILTER_TYPE, M_FILTER_OPERATION, M_FILTER_RESPONSE_TYPE, M_FILTER_SMOOTHNESS_TYPE, and M_FILTER_SMOOTHNESS operation control type settings.
-
Use MimConvolve() to specify the source and destination image buffers, as well as to specify a linear IIR filter context. Alternatively, use MimDifferential() to specify the source and destination image buffers for specific IIR operations that require more than one convolution.
Spatial filtering operations include operations such as smoothing, denoising, edge enhancement, and edge detection.
Spatial filtering operations compute results based on an underlying neighborhood process: the weighted sum of a pixel value and its neighbors' values. There are two types of spatial filters: Finite Impulse Response (FIR) filters and Infinite Impulse Response (IIR) filters. FIR filters operate on a finite neighborhood, while IIR filters take into account all values in an image. In MIL, you can specify either a predefined FIR spatial filter or a custom FIR or IIR spatial filter.
To apply custom FIR filters, you use MimConvolve(). To apply custom IIR filters, you use MimConvolve() or MimDifferential(), depending on the filter operation.
Finite Impulse Response (FIR) filters
For FIR filters, the weights are known as the kernel values. These kernel values determine the operation type of the spatial filter. For example, applying the following FIR filter results in a sharpening of the image:
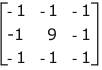
Whereas, applying the following FIR filter smooths an image (it also increases the intensity of the image by a factor of 16, so you will need to normalize the convolution result):

When using FIR filters, the dimensions of the kernel determine the size of the neighborhood that is used in the operation. The result of the operation is stored in the destination buffer at the location corresponding to the kernel's center pixel. When the kernel has an even number of rows and/or columns, the center pixel is considered to be the top-left pixel of the central elements in the neighborhood.

Calculate the X-coordinate of the top-left pixel of the central elements, as follows:
To calculate the Y-coordinate of the top-left pixel of the central elements, the same rules apply.
Regardless of the location of the center pixel, there will be some border pixels that have an incomplete neighborhood. To deal with this issue, the image buffer is overscanned. There are several types of overscan. A transparent overscan uses the parent buffer to provide the overscan pixels needed for the border calculation. If the parent buffer is not available, a mirror overscan is performed. A mirror overscan specifies that the overscan pixels will be a mirror copy of the source buffer's border pixels. A replicate overscan specifies to repeat border pixel values along each row and column of the overscan region. A replacement overscan allows you to specify a specific value for the overscan pixel values during processing. It is recommended that you experiment to find the best overscan option for your application. For more information on overscan, see the Buffer overscan region section of Chapter 21: Data buffers.
If the predefined FIR filters provided by MimConvolve() do not meet your requirements, you can create your own custom FIR filter. Before resorting to a custom filter, if speed is not an issue, try the bilateral adaptive filter M_BILATERAL, available using MimFilterAdaptive(), which uses a FIR filter. For more information, see the Adaptive filters subsection of the Denoise using spatial filtering and area open and close operations section of Chapter 3: Fundamental image processing.
To define your own custom FIR filter:
To apply your own custom FIR filter, call the MimConvolve() function, specifying the identifier of the required kernel buffer (FilterContextImOrKernelBufId).
To increase the speed of the convolution operation when using your custom FIR filter, MimConvolve() will automatically separate large kernels, if separable, into two 1-dimensional kernels (aij = hivj ). Performing two separate convolutions, once with Hmx1 and once with V1xn , can be faster and is equivalent to performing one convolution operation using the original Amxn kernel. MIL will internally separate large kernels when it detects that the separation results in better performance. The following displays an Amxn kernel separated into two 1-dimensional kernels (Hm and Vn ).

Infinite Impulse Response (IIR) filters
When using IIR filters, the weights are automatically determined by the type of filter, the mode of the filter, the type of operation to perform, and the degree of smoothness (strength of denoising) applied by the filter.
The type of filter determines the distribution of the neighborhoods' influence. MIL supports two types of IIR spatial filters: Deriche filter and Shen-Castan filter. For the Deriche filter, the neighborhoods' influence decreases much slower as the distance from the central pixel increases, compared to the Shen-Castan filter. For more information, see the Customizing the edge extraction settings section of Chapter 9: Edge Finder.
To define and use a custom IIR filter:
The following code snippet performs a smoothing operation using a Deriche custom IIR filter:
MIL_ID MilSystem = 0, /* System identifier. */
MilSrcImage = 0, /* Source image identifier */
MilDstImage = 0, /* Destination image identifier */
MilFilter = 0; /* Filter identifier. */
/* Smoothing the source image. */
/* Allocate the kernel. */
MimAlloc(MilSystem, M_LINEAR_FILTER_IIR_CONTEXT, M_DEFAULT, &MilFilter);
/* Set the kernel properties. */
MimControl(MilFilter, M_FILTER_TYPE, M_DERICHE);
MimControl(MilFilter, M_FILTER_SMOOTHNESS, 50.0);
MimControl(MilFilter, M_FILTER_OPERATION, M_SMOOTH);
/**/
/* Smooth the image. */
MimConvolve(MilSrcImage, MilDstImage, MilFilter);
/**/
/* Free the kernel. */
MimFree(MilFilter);
This second snippet performs first derivative calculations:
MIL_ID MilSystem = 0, /* System identifier. */
MilSrcImage = 0, /* Source image identifier */
MilDstDxImage = 0, /* X derivative destination image identifier */
MilDstDyImage = 0, /* Y derivative destination image identifier */
MilFilter = 0; /* Filter identifier. */
/* Calculate derivatives. */
/* Allocate the kernel. */
MimAlloc(MilSystem, M_LINEAR_FILTER_IIR_CONTEXT, M_DEFAULT, &MilFilter);
/* Set the kernel properties. */
MimControl(MilFilter, M_FILTER_TYPE, M_DERICHE);
MimControl(MilFilter, M_FILTER_SMOOTHNESS, 50.0);
MimControl(MilFilter, M_FILTER_RESPONSE_TYPE, M_SLOPE);
/**/
/* Extract relevant derivatives. */
MimControl(MilFilter, M_FILTER_OPERATION, M_FIRST_DERIVATIVE_X);
MimConvolve(MilSrcImage, MilDstDxImage, MilFilter);
MimControl(MilFilter, M_FILTER_OPERATION, M_FIRST_DERIVATIVE_Y);
MimConvolve(MilSrcImage, MilDstDyImage, MilFilter);
/**/
/* Free the kernel. */
MimFree(MilFilter);
An example
The following is an example of a spatial filtering operation using a custom FIR filter with a 3 by 3 kernel.