Warping

---

In addition to functions which perform specific geometric transforms (MimFlip(), MimResize(), MimRotate(), MimTranslate(), and MimPolarTransform()), MIL includes a more general geometric function, MimWarp(). It can perform any of the specific transforms, as well as complex warpings. Specifically, it can perform: first-order polynomial warpings, perspective polynomial warpings, and custom warpings.

Note that the functions which perform specific transforms are faster than MimWarp(). You should only use MimWarp() when the required transform cannot be otherwise performed. In addition, geometric distortions can also be resolved using the Camera Calibration module. For more information, see Chapter 25: Calibrating your camera setup.

MimWarp() performs a warping by first associating each pixel position of the destination buffer, (x_d, y_d), with a specific point (not necessarily a pixel) in the source buffer, (x_s, y_s). The pixel value at (x_d, y_d) is then determined from an interpolation around its associated source point. Destination pixels can be associated with source points in two different ways:

Using a 3x3 coefficients matrix that is used as follows:

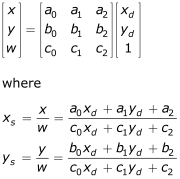
Using LUTs (an X-LUT and a Y-LUT) that are the same size as the destination image and are used as follows:

x _s = LUT_x[x _d, y _d].

y _s = LUT_y[x _d, y _d].

If you intend on performing the same warping operation on multiple images (which would require using the same LUTs), it might be faster to generate the LUTs for the operation once and repeatedly pass them to MimWarp(). However, if different warpings are required, or only one image is to be processed, it is faster to generate the coefficients and call MimWarp() than it is to generate the LUTs and call MimWarp().

A warping example, MimWarp.cpp, can be found in your examples directory.

First-order polynomial warpings

A first-order polynomial warping is equivalent to linearly translating, rotating, resizing, and/or shearing an image. First-order polynomial warpings are performed by associating points in the source buffer with pixels in the destination buffer according to the following equations:

x _s = a₀ x _d + a₁ y _d + a₂ .

y _s = b₀ x _d + b₁ y _d + b₂ .

To perform a first-order polynomial warping using a 3x3 coefficients matrix, you must pass the identifier of a 3x3 coefficients matrix buffer to MimWarp() in the WarpParam1BufId parameter. The elements of the last row of the coefficient matrix should be 0, 0, 1. The coefficients of this matrix can be generated automatically using MgenWarpParameter() or can be user supplied. When using MgenWarpParameter(), specify how to perform the warping (for example, specify by how much to rotate and resize an image); the function then generates the coefficients required to produce such a warping. To combine coefficients, use separate calls to MgenWarpParameter(). For example, to generate coefficients for a rotation and translation, call MgenWarpParameter() twice, using the output buffer of the first call as the input buffer of the second call. After all coefficients are generated, pass the coefficient buffer to MimWarp().

When performing a first-order polynomial warping using LUTs, you can customize the values in your LUTs or alternatively, you can generate the LUTs automatically with MgenWarpParameter(). To create the LUTs with the MgenWarpParameter() function, you can either pass the same information as when generating the coefficients or pass the 3x3 coefficients matrix, itself. After the LUTs are generated, pass them to MimWarp().

Perspective polynomial warpings

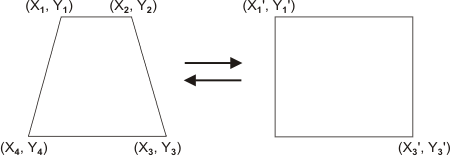
A perspective polynomial warping is used to map an arbitrary quadrilateral onto a rectangle or to map a rectangle onto an arbitrary quadrilateral.

Perspective polynomial warpings are performed by associating points in the source buffer with pixels in the destination buffer according to the following equations:

x _s = (a₀ x _d + a₁ y _d + a₂)/(c₀ x _d + c₁ y _d + c₂).

y _s = (b₀ x _d + b₁ y _d + b₂)/(c₀ x _d + c₁ y _d + c₂).

To perform a perspective polynomial warping using a 3x3 coefficients matrix, you must pass the identifier of a 3x3 coefficients matrix to MimWarp(). The coefficients of this matrix can be generated automatically using MgenWarpParameter() or can be user supplied. When using MgenWarpParameter(), you must specify the coordinates of the four corners of the quadrilateral or the two opposite corners of the rectangle. The coordinates are illustrated in the image below.

When performing a perspective polynomial warping using LUTs, you can customize the values in your LUTs or alternatively, you can generate the LUTs automatically with MgenWarpParameter(). To create the LUTs with the MgenWarpParameter() function, you can either pass the same information as when generating coefficients or pass the 3x3 coefficients matrix, itself. After the LUTs are generated, pass them to MimWarp().

Custom warpings

You can perform a custom warping using LUTs, since X_s and Y_s can be arbitrarily mapped. Load the X-LUT and Y-LUT with your custom values and pass them to MimWarp().

Interpolation modes

When you perform a warping, pixel positions in the destination buffer, (x_d, y_d), get associated with specific points in the source buffer, (x_s, y_s). The destination coordinates have integer values but the source coordinates, in general, do not. Therefore, the pixel value at (x_d, y_d) has to be determined from several source pixels that are near (x_s, y_s), according to a specified interpolation mode.

The following interpolation modes are available:

In general, nearest-neighbor interpolation is the fastest to perform, and bicubic interpolation is the slowest. However, nearest-neighbor interpolation produces the least accurate results, and bicubic interpolation produces the most accurate. Bilinear interpolation is often the best compromise between speed and accuracy.

Points outside the source buffer

Sometimes, the point associated with a destination pixel will fall outside the source buffer. In such cases, the new value for the destination pixel can be determined in one of the following ways:

In general, you should use pixels from the source buffer's ancestor buffer when the source buffer is a child buffer. This will ensure that the pixels you use are related to the source buffer. If the source buffer is not a child buffer, use one of the other options.

Note that you can set the destination pixel to a value other than 0 by first clearing the destination buffer to that value.