Inquiring about your camera calibration
- See also

 Availability
Availability 
 Previous
Previous
- Next

-
Inquire the original pixel coordinates of the calibration points using McalInquire() with M_CALIBRATION_IMAGE_POINTS_X and M_CALIBRATION_IMAGE_POINTS_Y.
-
Transform the original pixel coordinates to world coordinates using McalTransformCoordinate() or McalTransformCoordinateList() with M_PIXEL_TO_WORLD.
-
Inquire the original world coordinates of the calibration points using McalInquire() with M_CALIBRATION_WORLD_POINTS_X and M_CALIBRATION_WORLD_POINTS_Y.
-
Compare the transformed world coordinates to the original world coordinates to calculate your own world calibration error metrics. Calibrations in M_LINEAR_INTERPOLATION mode should have two nearly identical sets of coordinates.
-
To retrieve the position of the relative coordinate system, use McalInquire() with M_RELATIVE_ORIGIN_X, M_RELATIVE_ORIGIN_Y, and M_RELATIVE_ORIGIN_Z. To inquire about the rotation of the relative coordinate system, use McalInquire() with M_RELATIVE_ORIGIN_ANGLE; this will return the counter-clockwise angle of rotation about the Z-axis as measured with respect to the absolute coordinate system.
-
To retrieve the position of the tool coordinate system, use McalInquire() with M_TOOL_POSITION_X, M_TOOL_POSITION_Y, and M_TOOL_POSITION_Z.
-
To retrieve the calculated effective focal length of the modeled pinhole camera, use McalInquire() with M_FOCAL_LENGTH. The returned value is expressed in horizontal pixel units. You can use the following relation to convert the focal length from pixel units into real-world units:
Where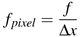
 specifies
the distance between the centers of two horizontally adjacent CCD
elements of your camera. Note that this is the focal length of the
modeled pinhole camera; it will not necessarily match the focal
length given by the lens manufacturer.
specifies
the distance between the centers of two horizontally adjacent CCD
elements of your camera. Note that this is the focal length of the
modeled pinhole camera; it will not necessarily match the focal
length given by the lens manufacturer. -
To retrieve the second order radial distortion coefficient, use McalInquire() with M_DISTORTION_RADIAL_1. Radial distortion refers to image distortions caused by the camera's lens, namely, pin cushion and barrel distortions. It is calculated by measuring the distance from the principal point to any other point in the image plane.
The second order radial distortion coefficient is used in calculations to remove lens distortion, as described below.
Let
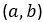 represent the distorted (acquired) pixel
coordinates.
represent the distorted (acquired) pixel
coordinates.Coordinates are normalized and centered using
 and the principal point
and the principal point 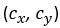 :
:
Let
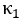 represent the second order radial distortion
coefficient.
represent the second order radial distortion
coefficient.
Where
 represent the corrected, undistorted
coordinates.
represent the corrected, undistorted
coordinates. -
To locate the camera's position in space, use McalGetCoordinateSystem() with M_CAMERA_COORDINATE_SYSTEM as a target coordinate system.
After camera calibration, you can inquire about the status and accuracy of your calibration, as well as the position and orientation of your coordinate systems. You can also inquire the intrinsic and extrinsic attributes of the pinhole camera used to model your camera when working with 3D-based camera calibration modes.
Camera calibration status and errors
After calibrating with McalGrid() or McalList(), you can check the success of your camera calibration using McalInquire() with M_CALIBRATION_STATUS. If calibration was successful, it will return M_CALIBRATED, otherwise an error code is returned. For example, if you calibrate using McalGrid() and the grid does not meet the required guidelines, M_CALIBRATION_STATUS returns M_GRID_NOT_FOUND. If you try to perform a full calibration in M_TSAI_BASED mode, and the camera is placed perpendicular to the grid, M_PLANE_ANGLE_TOO_SMALL is returned.
M_NOT_INITIALIZED is returned if M_CALIBRATION_STATUS is inquired before calling McalGrid() or McalList().
Camera calibration accuracy
After a successful camera calibration, you can inquire about the accuracy of your calibration. From the pixel coordinates and corresponding world coordinates of the calibration points, McalGrid() and McalList() establishes a mapping function that can transform any pair of pixel coordinates to their corresponding world coordinates, and vice versa. Depending on several factors, such as the calibration mode, noise in the image, and camera distortion, the mapping function might not be perfectly accurate. After calibration, this slight inaccuracy can even apply to the original calibration points. For instance, the original pixel coordinates of the calibration points, when transformed into world coordinates, might not equal the original world coordinates of the calibration points. The difference between the transformed coordinates and the original coordinates of the calibration points is called camera calibration error.
In the default M_LINEAR_INTERPOLATION calibration mode, the mapping function is created such that the pixel coordinates, when transformed into world coordinates, are nearly identical to the original world coordinates, and vice versa, for all calibration points. This results in a camera calibration that is nearly perfectly accurate for the calibration points. When calibrating using a grid, this implies a very high accuracy in the area of the image with the grid, and a lower accuracy for the rest of the image. In every other calibration mode, the mapping function is created, such that it is accurate more evenly across the entire image. Effectively, this means that in M_LINEAR_INTERPOLATION calibration mode, real-world measurements will be more accurate the closer they are to the area of the image that had the grid; while in all other calibration modes, any inaccuracy of real-world measurements will be felt equally throughout the image.
You can inquire about the camera calibration error using McalInquire() with M_AVERAGE_PIXEL_ERROR, M_MAXIMUM_PIXEL_ERROR, M_AVERAGE_WORLD_ERROR, or M_MAXIMUM_WORLD_ERROR.
Note that for robotics camera calibration mode, you can use McalInquireSingle() to inquire about the calibration accuracy of each call to McalGrid() or McalList() made with M_ACCUMULATE.
There are two main causes of calibration error: problems finding calibration points and problems creating the mapping function.
Addressing calibration error due to problems finding calibration points
McalGrid() takes an image of a grid and determines the pixel coordinates of the calibration points using feature extraction algorithms. You can assess the accuracy of the feature extraction using McalDraw() with M_DRAW_IMAGE_POINTS, which draws the extracted calibration points. You can overlay the extracted calibration points on the original image of the grid to ensure that there are no false calibration points or missing calibration points. It is also important that the pixel coordinates of the calibration points are directly in the middle of each circle, for a circle grid, or at the intersection of the grid squares, for a chessboard grid or fiducial grid. Any extra points, missing points, or imprecisely positioned points will result in calibration error.
You can typically improve the accuracy of the found calibration points by physically cleaning your grid or cleaning up the image of the grid. Cleaning up the image of the grid can include adjusting the focus of the camera, the saturation of the image, or the lighting in the setup. The contrast between the foreground and the background of the grid must be sharp.
Addressing calibration error due to problems creating the mapping function
Camera calibration creates a mapping function that can transform pixel coordinates to world coordinates, and vice versa. This mapping function makes certain assumptions, based on the calibration mode. Any violation of the assumptions can result in a mapping function that imprecisely maps pixel coordinates to world coordinates. For instance, camera calibrations calculated in M_PERSPECTIVE_TRANSFORMATION mode cannot be used with cameras that have lens distortion. If you calibrated your camera setup in this mode and your camera has lens distortion, there would likely be mapping problems.
Often the violation of assumptions is a matter of degree. For instance, most cameras have at least a small amount of lens distortion, especially around the edge of the lens. This means that most calibrations calculated using M_PERSPECTIVE_TRANSFORMATION mode (which doesn't compensate for lens distortion) will have some degree of calibration error.
You can determine if the error is within tolerance using McalInquire(). There are two types of calibration error measured: pixel error (M_AVERAGE_PIXEL_ERROR or M_MAXIMUM_PIXEL_ERROR) and world error (M_AVERAGE_WORLD_ERROR and M_MAXIMUM_WORLD_ERROR). The pixel error is the pixel difference between the original world coordinates of the calibration points transformed into pixel coordinates, and the original pixel coordinates of the calibration points. The world error is the world difference between the original pixel coordinates of the calibration points transformed into world coordinates, and the original world coordinates of the calibration points. In both cases, the calibration error is a measure of the quality of the mapping function as applied to the calibration points.
You can visually inspect the location and severity of the calibration error using McalDraw(). You can draw the original pixel coordinates of the calibration points using M_DRAW_IMAGE_POINTS, and you can draw the original world coordinates of the calibration points, transformed into the pixel coordinates with the mapping function, using M_DRAW_WORLD_POINTS. By drawing the original and transformed coordinates together, you can see where the points differ. This difference is calibration error. Alternatively, you could draw just the original world coordinates (transformed into pixel coordinates with the mapping function), directly on the image of the original grid, as in the image below. This way you can see exactly where on the grid are the biggest differences. With this information, you can adjust the setup as needed.

To improve the accuracy of your calibration (reduce the calibration error caused by mapping problems), you can specify a calibration mode that better represents the assumptions of your camera setup. Generally speaking, you can reduce camera calibration error by calibrating again using a new camera calibration context that encompasses more assumptions. If your first calibration mode is M_UNIFORM_TRANSFORMATION and it produces a calibration with more calibration error than you can tolerate, try using a new calibration context in M_PERSPECTIVE_TRANSFORMATION mode. If this still produces a calibration with more error than is tolerable, try using a new calibration context in M_TSAI_BASED mode. Note that M_TSAI_BASED mode supports 3D calibration and has additional setup considerations.
In the default calibration mode, M_LINEAR_INTERPOLATION mode, the mapping function is created so that comparing transformed coordinates (either pixel-to-world or world-to-pixel) to the original coordinates of the calibration points results in almost no measured calibration error. This produces increased calibration accuracy for areas of the image inside the grid and reduced accuracy for areas outside the grid. Because calibration error is measured using calibration points, there is no way to measure the inaccuracy of the areas outside of the grid. Also, if the pixel coordinates or world coordinates of any calibration point are incorrectly specified, the mapping will be significantly inaccurate in the area around the incorrectly specified calibration point. This inaccuracy also cannot measured.
For information on each calibration mode, including a list of supported features, see the Uniform camera calibration and other camera calibration modes section earlier in this chapter.
Another way to improve the accuracy of the mapping function is to increase the number of calibration points used to calibrate your camera setup. When calibrating using a grid, this means you could use a grid with more columns or rows, possibly with smaller spacings between calibration points. The number of calibration points and the size of the spacings has limitations, which are discussed in the Calibrating using calibration points from a grid section earlier in this chapter. To maximize grid coverage in your image, you can use a chessboard or fiducial grid that extends outside the image borders, using McalControl() with M_GRID_PARTIAL set to M_ENABLE.
Inquiring pixel and world calibration points
You can inquire the pixel coordinates and world coordinates of the calibration points that were used by McalGrid() or McalList() to create the camera calibration.
If you have calibrated using McalGrid(), the pixel coordinates of the calibration points are those automatically extracted from the image of the grid, and the world coordinates of the calibration points are those calculated from the world description of the grid (number and spacings of the rows and columns of the grid). If you have calibrated using McalList(), you have explicitly specified the pixel coordinates and world coordinates of the calibration points.
You can inquire the pixel coordinates of the calibration points, using McalInquire() with M_CALIBRATION_IMAGE_POINTS_X and M_CALIBRATION_IMAGE_POINTS_Y. When inquiring the pixel coordinates of calibration points from a grid, the coordinates correspond to the extracted center of the circles in a circle grid or to the extracted intersections of four corners in a chessboard grid or fiducial grid.
You can inquire the world coordinates of the calibration points, using McalInquire() with M_CALIBRATION_WORLD_POINTS_X and M_CALIBRATION_WORLD_POINTS_Y.
You can use these coordinates to independently calculate calibration error. To calculate the calibration error in world units, perform the following:
Note that to calculate the calibration error in pixel units, you must perform the same steps but in a different order. First you must inquire the original world coordinates, then transform them to pixel coordinates with M_WORLD_TO_PIXEL, then inquire the original pixel coordinates, and finally compare the transformed pixel coordinates with the original pixel coordinates to calculate the pixel calibration error.
Position and orientation of coordinate systems
You might need to inquire about the position and orientation of one coordinate system with respect to another. You can do so using McalInquire() for two-dimensional camera calibration modes or McalGetCoordinateSystem() for three-dimensional camera calibration modes.
For two dimensional camera calibration modes, you can inquire about the position and orientation of the relative coordinate system and the position of the tool coordinate system:
For 3D-based camera calibration modes, use McalGetCoordinateSystem() to inquire about the position and orientation of the absolute, relative, tool, or camera coordinate systems. For robotics camera calibration mode, you can also inquire about the position and orientation of the robot base coordinate system.
McalGetCoordinateSystem() can return the relationship between these coordinate systems in three-dimensional space, in terms of a specified type of transformation. For example, after a successful Tsai-based camera calibration, you might need to know the calculated position and orientation of your camera with respect to the absolute coordinate system. To obtain this information as a translation and rotation of the camera coordinate system from the absolute coordinate system, you can use McalGetCoordinateSystem() with M_CAMERA_COORDINATE_SYSTEM as the target coordinate system and M_ABSOLUTE_COORDINATE_SYSTEM as the reference coordinate system. The following code snippet shows how to retrieve this information using two consecutive calls to McalGetCoordinateSystem(). The first call returns the X-, Y-, and Z-coordinates of the camera coordinate system's origin, and the second call returns the three rotation angles of the camera coordinate system's axes around the X-, Y-, and Z-axes of the absolute coordinate system.
/*
Get the position and orientation of the camera
with respect to the absolute coordinate system.
*/
MIL_DOUBLE CameraPosX, CameraPosY, CameraPosZ;
MIL_DOUBLE AngleY, AngleX, AngleZ;
McalGetCoordinateSystem(CalibrationID,
M_CAMERA_COORDINATE_SYSTEM,
M_ABSOLUTE_COORDINATE_SYSTEM,
M_TRANSLATION,
M_NULL, &CameraPosX, &CameraPosY, &CameraPosZ, M_NULL);
McalGetCoordinateSystem(CalibrationID,
M_CAMERA_COORDINATE_SYSTEM,
M_ABSOLUTE_COORDINATE_SYSTEM,
M_ROTATION_YXZ,
M_NULL, &AngleY, &AngleX, &AngleZ, M_NULL);
For robotics camera calibration mode, you can retrieve the position and orientation of any coordinate system with respect to the robot base coordinate system using McalGetCoordinateSystem(). The values returned can then be provided to a robot controller software to move the robot.
Note that the pixel coordinate system cannot be used with McalGetCoordinateSystem(). Refer to the Working with real-world units section earlier in this chapter for information on transforming values from world to pixel units.
Refer to the Moving coordinate systems to reflect camera setup changes section later in this chapter for more information on coordinate system transformations.
Pinhole camera
You can retrieve the values of several intrinsic and extrinsic attributes of the pinhole camera used to model your camera when working in Tsai-based or robotics camera calibration mode: